题目内容
如图，已知
ABCD。
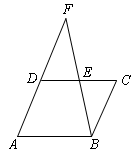
（1）作图：延长BC，并在BC的延长线上截取线段CE，使得CE=BC（用尺规作图法，保留作图痕迹，不要求写
作法）；
（2）)在（1）的条件下，连结AE，交CD于点F，求证：△AFD≌△EFC。
ABCD。（1）作图：延长BC，并在BC的延长线上截取线段CE，使得CE=BC（用尺规作图法，保留作图痕迹，不要求写
作法）；
（2）)在（1）的条件下，连结AE，交CD于点F，求证：△AFD≌△EFC。
解：（1）如图所示：
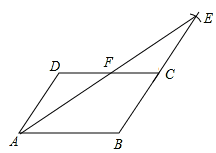
（2）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC。
∵BC=CE，
∴AD=CE。
∵AD∥BC，
∴∠DAF=∠CEF。
在△ADF和△ECF中，
∵
，
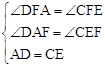∴△ADF≌△ECF（AAS）。
（2）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC。
∵BC=CE，
∴AD=CE。
∵AD∥BC，
∴∠DAF=∠CEF。
在△ADF和△ECF中，
∵
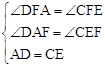，∴△ADF≌△ECF（AAS）。
试题分析：（1）根据题目要求画出图形即可。
（2）首先根据平行四边形的性质可得AD∥BC，AD=BC，进而得到AD=CE，∠DAF=∠CEF，进而可利用AAS证明△AFD≌△EFC。
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
ABCD的边CD的中点，AD、BE的延长线相交于点F，DF=3，DE=2，则
