题目内容
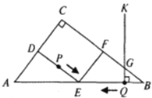
【题目】如图,G是正六边形ABCDEF的边CD的中点,连接AG交CE于点M,则GM:MA=______.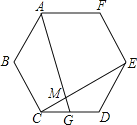
【答案】1:6.
【解析】
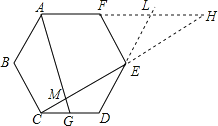
延长CE交AF的延长线于H,延长DE交AF延长线于L,根据正六边形的内角和定理可求出各内角的度数,利用平角的性质及等边三角形的性质可求出△FEL是等边三角形;再根据AAS定理求出△CDE≌△HLE,可得出AF=FL=HL,再利用AF∥CD可得△CGM∽△HAM,由三角形的相似比即可求解.
延长CE交AF的延长线于H,延长DE交AF延长线于L;
∵∠AFE=∠FED=∠CDE=![]() =120°,
=120°,
∴∠LFE=∠FEL=180°-120°=60°,
∴AF=EF=FL=EL;
∵∠HLE是△EFL的外角,
∴∠HLE=∠LFE+∠FEL=120°,
∴∠HLE=∠CDE;
∵∠CED=∠FEH,DE=EL,
∴△CDE≌△HLE,
∴CD=HL,
∴AH=3AF=3CD;
∵G是CD的中点,即CG=![]() CD,
CD,
∴CG:AH=![]() :3=1:6.
:3=1:6.
∵AF∥CD,
∴△CGM∽△HAM,GM:AM=CG:AH=![]() :3=1:6.
:3=1:6.
故答案为:1:6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目