题目内容
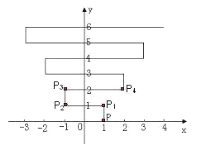
【题目】如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是_________.
【答案】(-505,1010).
【解析】
解决本题的关键是根据图形,写出各点坐标,利用具体数值分析出题目的规律,再进一步解答.注意到第奇数次都是向上跳一个单位,而偶数次跳的次数也是有规律的.
由题中规律可得出如下结论:设点Pm的横坐标的绝对值是n,
则在y轴右侧的点的下标分别是4(n1)和4n3,
在y轴左侧的点的下标是:4n2和4n1;
∵2019=505×4-1,2020=4×(506-1),
∴点P2019的横坐标为-505.
∵点P1和点P2的纵坐标均为1,点P3和点P4的纵坐标均为2,点P5和点P6的纵坐标均为3,
因此可以推出,点P2019和点P2020的纵坐标均为2020÷2=1010,
∴点P第2019次跳动至点P2019的坐标是(-505,1010).
故答案为:(-505,1010).

练习册系列答案
相关题目