题目内容
【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
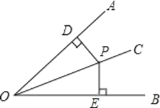
已知:如图,OC是∠AOB的角平分线,点 P 在 OC 上, 求证: .
(要求:请你补全已知和求证,并写出证明过程.)
【答案】PD⊥OA于D,PE⊥OB于E,PD=PE.证明见解析.
【解析】
根据题意、结合图形写出已知和求证,证明△OPD≌△OPE,根据全等三角形的性质即可得到结论.
已知:如图,OC是∠AOB的角平分线,点P在OC上,PD⊥OA于D,PE⊥OB于E,求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
∵OC是∠AOB的角平分线,
∴∠AOC=∠BOC
在△PDO和△PEO中,
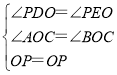 ,
,
∴△PDO≌△PEO(AAS),
∴PD=PE.
故答案为:PD⊥OA于D,PE⊥OB于E,PD=PE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目