题目内容
【题目】如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
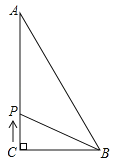
(1)当t= 时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是![]() = .
= .
(3)若△BPC的面积为18,试求t的值.
【答案】(1)6.5秒;(2)1:4;(3)t=![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,列出方程求解即可;
(2)求出当t=5时,AP与BP的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①P在AC上;②P在AB上,分别根据三角形面积公式建立关于t的方程,求解可得.
解:(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,
此时CA+AP=12+7.5=19.5,
∴3t=19.5,
解得t=6.5,
故当t=6.5秒时,CP把△ABC的面积分成相等的两部分;
(2)∵5×3=15,
∴AP=1512=3,BP=153=12,
则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BPC的面积为18,
∴![]() ×9×CP=18,
×9×CP=18,
∴CP=4,
∴3t=4,t=![]() ;
;
②当P在AB上时,
∵△BPC的面积为18,△ABC的面积为![]() ,
,
∴△BPC的面积是△ABC面积的![]() ,
,
∴3t=12+15×![]() ,
,
解得:t=![]() ,
,
故t=![]() 秒或
秒或![]() 秒时,△BPC的面积为18.
秒时,△BPC的面积为18.

【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.