题目内容
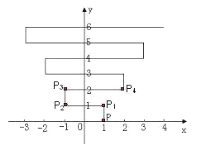
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+|b+3|=0,S△ABC=14。

(1)求C点的坐标
(2)作DE⊥DC交y轴于E点,EF为∠AED的平分线,且∠DFE=90o。求证:FD平分∠ADO.
【答案】(1)(4,-3);(2)见解析;
【解析】
(1)根据平方根的性质和绝对值的非负性,求出a,b的值,再根据三角形面积公式即可解答.
(2)根据角平分线的性质,三角形的内角和定理,分别求出∠OEG=∠FDG和∠ADF=∠AEF即可求证.
(1)∵(a-4)2+|b+3|=0,
∴a=4,b=-3.
又∵S△ABC =14,
∴![]() × AB×BO=14,
× AB×BO=14,
∵AB=7
∴BC=4,C点的坐标为(4,-3);
(2)设OD与EF相交于点G,

∵∠F=90°,∠EOG=90°,
∴∠EGO=∠FGD,
∴∠OEG=∠FDG①,
∵∠ADE=90°,
∴∠ADF+∠FDE=90°,在△EFD中,∠FDE+∠FED=90°,
∴∠ADF=∠FED,
又∵EF平分∠AED,
∴∠AEF=∠FED,∴∠ADF=∠AEF②,
由①②得∠FDG=∠ADF,
∴FD平分∠ADO.

练习册系列答案
相关题目