��Ŀ����
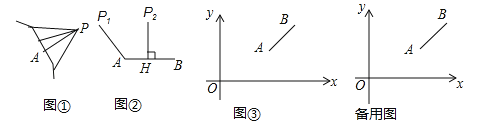
����Ŀ����ͼ����������������A��B����![]() ��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
![]()
��1��д�������ϵ�B��ʾ����______����P��ʾ�����ú�t��ʽ�ӱ�ʾ��_______��
��2�����M��AP���е㣬��N��PB���е�.��P��ֱ��AB���˶��Ĺ����У��߶�MN�ij����Ƿ�ᷢ���仯���������仯����˵�����ɣ������仯������߶�MN�ij���.
��3������R�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Rͬʱ����������P�˶�������ʱ�����R�ľ���Ϊ2����λ����.
���𰸡���1��-14��6-4t����2���߶�MN�ij��Ȳ������仯��MN�ij���Ϊ10cm����3����P�˶�11���9��ʱ�����R�ľ���Ϊ2����λ����.
��������
��1�����ݵ�B�ڵ�A����༰�������������빫ʽ���ɵó���B��ʾ���������þ���=�ٶ���ʱ��ɱ�ʾAP�ľ��룬���ɱ�ʾ����P��ʾ������
��2�������е�Ķ�������AM��BN�ij�������MN=AB-BN-AM�������MN�ij������ɵô𰸣�
��3�����þ���=�ٶ���ʱ��ɵó���R�͵�P��ʾ�����������������������빫ʽ�з������tֵ����.
��1���ߵ�![]() ��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20��
��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20��
���B��ʾ����Ϊ6-20=-14��
�߶���P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶���
���P��ʾ����Ϊ6-4t��
�ʴ�Ϊ��-14��6-4t
��2����ͼ���ߵ�M��AP���е㣬��P���ٶ�Ϊÿ��4����λ���ȣ�
��AM=![]() ��4t=2t��
��4t=2t��
�ߵ�N��PB���е㣬
��BN=![]() ��(20-4t)=10-2t��
��(20-4t)=10-2t��
��MN=AB-BN-AM=20-(10-2t)-2t=10��
![]()
���P��ֱ��AB���˶��Ĺ����У��߶�MN�ij��Ȳ������仯��MN�ij���Ϊ10cm.
��3���߶���R�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶���
���R��ʾ������-14-2t��
�ߵ�P��ʾ����Ϊ6-4t����P���R�ľ���Ϊ2����λ����.
��PR=![]() =2����
=2����![]() =2��
=2��
��ã�t=11��t=9��
���P�˶�11���9��ʱ�����R�ľ���Ϊ2����λ����.

����Ŀ��ij����ÿ��������Ҫ����һ��Ѫѹ���±��Ǹò��˱�������һ������������ѹ�ı仯���.����������ʾ��������������ʾ�½���
���� | һ | �� | �� | �� | �� |
����ѹ�ı仯����ǰһ��Ƚϣ� | +30 | -20 | +17 | +18 | -20 |
��1������������һ��Ƚ�����ѹ________�ˣ�������������½�����
��2��ͨ������˵������������ѹ������������������˻����½��ˣ�������������½��˶��٣�
��3������ò��˱����������ѹΪ185����ô���ϸ����յ�����ѹΪ���٣�