题目内容
【题目】1883年，康托尔构造的这个分形，称做康托尔集，从长度为1的线段开始，康托尔取走其中间三分之一而达到第一阶段；然后从每人个余下的三分之一线段中取走中间三分之一而达到第二阶段，无限地重复这一过程，余下的无穷点就称做康托尔集，下图是康托尔集的最初几个阶段，当达到第5个阶段时，取走的所有线段的长度之和为（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据题意具体表示出前几个式子，然后推广到一般情形，发现规律解决问题．
解：根据题意知：第一阶段时，余下的线段的长度之和为
，
第二阶段时，余下的线段的长度之和为×＝
，
第三阶段时，余下的线段的长度之和为××＝
，
…
以此类推，
第5个阶段时，余下的线段的长度之和为
，则取走的所有线段的长度之和为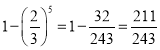
，
故选：C.
练习册系列答案
考前必练系列答案
相关题目
