题目内容
【题目】在平面直角坐标系中，如果点P 的横坐标和纵坐标相等，则称点P为和谐点。
（1）求函数
的图像上和谐点的坐标；
（2）若二次函数y＝ax2+4x+c（a≠0）的图象上有且只有一个和谐点（
，），当0≤x≤m时，函数y＝ax2+4x+c﹣
（a≠0）的最小值为﹣3，最大值为1，则m的取值范围.
【答案】（1）
；（2）2≤m≤4
【解析】
（1）根据和谐点的横坐标与纵坐标相同，设和谐点的坐标为（a,a）,代入
可得关于a的方程，解方程可得答案．
（2）根据和谐点的概念令ax2+4x+c=x，即ax2+3x+c=0，由题意，△=32-4ac=0，即4ac=9，方程的根为
＝
，从而求得a=-1，c＝
，所以函数y=ax2+4x+c-
=-x2+4x-3，根据函数解析式求得顶点坐标与纵坐标的交点坐标，根据y的取值，即可确定x的取值范围．
（1）设和谐点的坐标为（a,a），则a=-2a+1
解得：a=
，
∴函数的图像上和谐点的坐标为.
（2）令ax2+4x+c＝x，即ax2+3x+c＝0，
由题意，△＝32﹣4ac＝0，即4ac＝9，
又方程的根为
，
解得a＝﹣1，c＝
．
故函数y＝ax2+4x+c﹣＝﹣x2+4x﹣3，
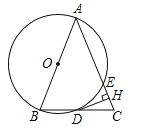
如下图，该函数图象顶点为（2，1），与y轴交点为（0，﹣3），由对称性，该函数图象也经过点（4，﹣3）．
由于函数图象在对称轴x＝2左侧y随x的增大而增大，在对称轴右侧y随x的增大而减小，且当0≤x≤m时，函数y＝﹣x2+4x﹣3的最小值为﹣3，最大值为1，
∴2≤m≤4.
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式.（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
