题目内容
【题目】(2017江苏省泰州市,第25题,12分)阅读理解:
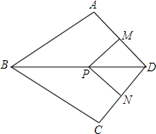
如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段PA1最短,则线段PA1的长度称为点P到图形l的距离.
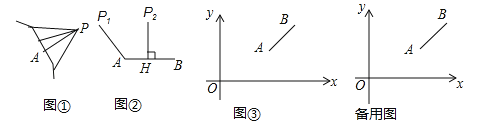
例如:图②中,线段P1A的长度是点P1到线段AB的距离;线段P2H的长度是点P2到线段AB的距离.
解决问题:
如图③,平面直角坐标系xOy中,点A、B的坐标分别为(8,4),(12,7),点P从原点O出发,以每秒1个单位长度的速度向x轴正方向运动了t秒.
(1)当t=4时,求点P到线段AB的距离;
(2)t为何值时,点P到线段AB的距离为5?
(3)t满足什么条件时,点P到线段AB的距离不超过6?(直接写出此小题的结果)
【答案】(1)![]() ;(2)t=5或t=11;(3)8﹣
;(2)t=5或t=11;(3)8﹣![]() ≤t≤
≤t≤![]() .
.
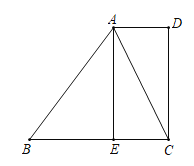
【解析】试题分析:(1)作AC⊥x轴,由PC=4、AC=4,根据勾股定理求解可得;
(2)作BD∥x轴,分点P在AC左侧和右侧两种情况求解,P位于AC左侧时,根据勾股定理即可得;P位于AC右侧时,作AP2⊥AB,交x轴于点P2,证△ACP2≌△BEA得AP2=BA=5,从而知P2C=AE=3,继而可得答案;
(3)分点P在AC左侧和右侧两种情况求解,P位于AC左侧时,根据勾股定理即可得;点P位于AC右侧且P3M=6时,作P2N⊥P3M于点N,知四边形AP2NM是矩形,证△ACP2∽△P2NP3得![]() ,求得P2P3的长即可得出答案.
,求得P2P3的长即可得出答案.
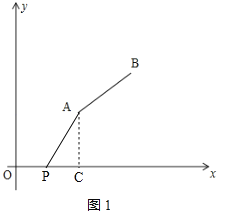
试题解析:解:(1)如图1,作AC⊥x轴于点C,则AC=4、OC=8,当t=4时,OP=4,∴PC=4,∴点P到线段AB的距离PA=![]() =
=![]() =
=![]() ;
;
(2)如图2,过点B作BD∥x轴,交y轴于点D.
①当点P位于AC左侧时,∵AC=4、P1A=5,∴P1C=![]() =
=![]() =3,∴OP1=5,即t=5;
=3,∴OP1=5,即t=5;
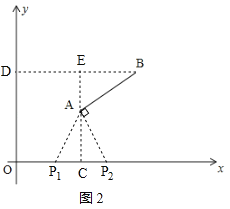
②当点P位于AC右侧时,过点A作AP2⊥AB,交x轴于点P2,∴∠CAP2+∠EAB=90°,∵BD∥x轴、AC⊥x轴,∴CE⊥BD,∴∠ACP2=∠BEA=90°,∴∠EAB+∠ABE=90°,∴∠ABE=∠P2AC,在△ACP2和△BEA中,∵∠ACP2=∠BEA=90°,AE=BE,∠P2AC=∠ABE,∴△ACP2≌△BEA(ASA),∴AP2=BA=![]() =
=![]() =5,而此时P2C=AE=3,∴OP2=11,即t=11;
=5,而此时P2C=AE=3,∴OP2=11,即t=11;
综上所述:t=5或t=11.
(3)如图3,①当点P位于AC左侧,且AP3=6时,则P3C=![]() =
=![]() =
=![]() ,∴OP3=OC﹣P3C=8﹣
,∴OP3=OC﹣P3C=8﹣![]() ;
;
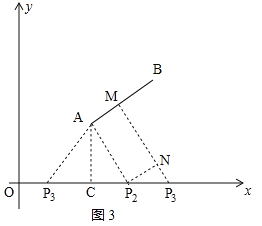
②当点P位于AC右侧,且P3M=6时,过点P2作P2N⊥P3M于点N,则四边形AP2NM是矩形,∴∠AP2N=90°,∠ACP2=∠P2NP3=90°,AP2=MN=5,∴△ACP2∽△P2NP3,且NP3=1,∴![]() ,即
,即![]() ,∴P2P3=
,∴P2P3=![]() ,∴OP3=OC+CP2+P2P3=8+3+
,∴OP3=OC+CP2+P2P3=8+3+![]() =
=![]() ,∴当8﹣
,∴当8﹣![]() ≤t≤
≤t≤![]() 时,点P到线段AB的距离不超过6.
时,点P到线段AB的距离不超过6.

 考前必练系列答案
考前必练系列答案