题目内容
【题目】如图,在△ABC中,∠ACB=900,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.

(1)求证:DE=EF;
(2)连接CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
【答案】(1)见解析.
(2)见解析.
【解析】
(1)通过由ASA证明△AED≌△CEF得出结论.
(2)如图,经过转换,将∠B转换成∠ADE,从而通过证明∠DGC=∠1和∠2=∠A得出结论.
证明:(1)∵在△ABC中,∠ACB=900,点D为边AB的中点,
∴DC=DA(直角三角形斜边上中线等于斜边的一半).
∵DE∥BC,∴AE=CE(平行线等分线段的性质),∠A=∠FCE(平行线的内错角相等).
又∵∠AED=∠CEF(对顶角相等),∴△AED≌△CEF(ASA).
∴DE=EF(全等三角形对应边相等).
(2)如图,∵在△ABC中,∠ACB=900,点D为边AB的中点,
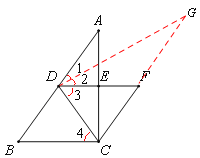
∴DC=DB(直角三角形斜边上中线等于斜边的一半).
∴∠B=∠4(等边对等角).
又∵DE∥BC,∴∠4=∠3,∠B=∠ADE.
∵DG⊥DC,∴∠2+∠3=900,即∠2+∠D=900.
∵∠ACB=900,∴∠A+∠D=900.∴∠2=∠A.
∵CF∥AB,∴∠DGC=∠1.
∴∠B=∠ADE=∠2+∠1=∠A+∠DGC.

练习册系列答案
相关题目