题目内容
如图△ABC中,AB=AC,EF∥BC,且⊙O内切于四边形BCFE.
(1)当
=
时,sinB=______;
(2)当
=
时,sinB等于多少?请说明理由.

(1)当
| AE |
| BE |
| 1 |
| 2 |
(2)当
| AE |
| BE |
| 1 |
| n |

连接AO并延长交EF于点D,交BC于点H,则AH⊥BC,连接OG,则OG⊥AB
(1)∵∠BAH+∠AOG=90°,∠B+∠BAH=90°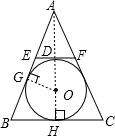
∴∠AOG=∠B,
∵EF∥BC
∴
=
=
设⊙O的半径为r,则
=
∵AD=
=r
∴AO=2r
又∵OG=r
∴AG=
=
r
∴sinB=
;
(2)sinB=
.
设AB与⊙O相切于点G,连接OG,则OG⊥AB
∴∠AOG=∠B
∵EF∥BC
∴
=
=
设⊙O的半径为r,则
=
∵AD=
∴AO=AD+r=
r
又∵OG=r
∴AG=
=
=
r
∴sinB=sin∠AOG=
=
=
.
(1)∵∠BAH+∠AOG=90°,∠B+∠BAH=90°

∴∠AOG=∠B,
∵EF∥BC
∴
| AD |
| DH |
| AE |
| EB |
| 1 |
| 2 |
设⊙O的半径为r,则
| AD |
| 2r |
| 1 |
| 2 |
∵AD=
| 2r |
| 2 |
∴AO=2r
又∵OG=r
∴AG=
| (2r)2-r2 |
| 3 |
∴sinB=
| ||
| 2 |
(2)sinB=
2
| ||
| n+2 |
设AB与⊙O相切于点G,连接OG,则OG⊥AB
∴∠AOG=∠B
∵EF∥BC
∴
| AD |
| DH |
| AE |
| EB |
| 1 |
| n |
设⊙O的半径为r,则
| AD |
| 2r |
| 1 |
| n |
∵AD=
| 2r |
| n |
∴AO=AD+r=
| n+2 |
| n |
又∵OG=r
∴AG=
| AO2-OG2 |
(
|
2
| ||
| n |
∴sinB=sin∠AOG=
| AG |
| AO |
| ||||
|
2
| ||
| n+2 |

练习册系列答案
相关题目


 作⊙O.
作⊙O.



 连接DE.
连接DE.