Question

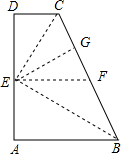
如图，在梯形ABCD中，AB∥DC．
①若∠A=90°，AB+CD=BC，则以AD为直径的圆与BC相切；
②若∠A=90°，当以AD为直径的圆与BC相切，则以BC为直径的圆也与AD相切；
③若以AD为直径的圆与BC相切，则AB+CD=BC；
④若以AD为直径的圆与BC相切，则以BC为直径的圆与AD相切．
以上判断正确的个数有（　　）

A．1

B．2

C．3

D．4

Answer 1

①作AD的中点E，作EG⊥BC于点G，过E作AB的平行线EF，则EF是梯形ABCD的中位线，
∴EF=

1

2

（AB+CD）=

1

2

BC=CF，
∴∠CEF=∠ECF，
∵EF∥CD，
∴∠DCE=∠CEF，
∵在△DCE和△GCE中，

∠DCE=∠ECF ∠D=∠CGE EC=EC

，
∴△DCE≌△GCE（AAS），
∴EG=DE=

1

2

AD，则以AD为直径的圆与BC相切．
故命题正确；
②若∠A=90°，当以AD为直径的圆与BC相切，设以AD为直径的圆的圆心是E，则E是AD的中点，设圆与BC相切与点G，
则连接EG，则EG⊥BC，且EG=ED．
∵在Rt△DCE和Rt△GCE中，

EG=ED EC=EC

，
∴Rt△DCE≌Rt△GCE（HL），
∴CG=CD，
同理，BG=AB，
∴AB+CD=BC，
取BC的中点，连接EF，则EF是梯形ABCD的中位线，
∴EF=

1

2

（AB+CD）=

1

2

BC，
又∵若∠A=90°，则EF⊥AD，
∴以BC为直径的圆也与AD相切．故②正确；
③需要∠A=90°，故错误．
④由面积法，可得以AD为直径的圆与BC相切，则以BC为直径的圆与AD相切．正确．
故正确的是：①②④．故选C．