Question

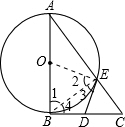
如图所示，△ABC是直角三角形，∠ABC=90°，以AB为直径的⊙O交AC于E点，点D是BC边的中点，连接DE．
（1）请判断DE与⊙O是怎样的位置关系？请说明理由．
（2）若⊙O的半径为4，DE=3，求AE的长．

Answer 1

（1）相切．
证明：连接OE，BE，
∵AB是⊙O的直径，
∴∠AEB=90°，
∴BE⊥AC，
∴在Rt△BEC中，点D是BC边的中点，
∴DE=BD=CD=

1

2

BC，
∴∠3=∠4，
∵∠ABC=90°，OB=OE，
∴∠1=∠2，∠1+∠4=90°，
∴∠2+∠3=90°，
∴DE⊥OE，
∴DE是⊙O的切线；

（2）∵∠AEO+∠2=90°，∠2+∠3=90°，
∴∠AEO=∠3，
∵OA=OE，
∴∠A=∠AEO，
∵∠3=∠4，
∴∠AEO=∠4，
∴△AEO∽△EBD，
∴

OA

DE

=

AE

BE

，
设AE=x，则BE=

AB2-AE2

=

64-x2

，
∴

4

3

=

x

64-x2

，
∴x=6.4．
∴AE=6.4．