��Ŀ����
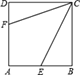
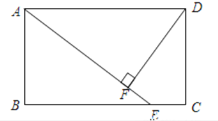
����Ŀ����ͼ��AB�Ǵ�ֱ��ˮƽ���һ����¥�����¥20�ף�BC��20�ף�Զ�ĵط���һ��б��CD���¶�Ϊ1��0.75�������³�CD��10�ף�ij������һ��ʱ�̣���̫���������£���¥��Ӱ��������ˮƽ��BC��б��CD���Լ��¶��ϵ�ˮƽ��DE����A��B��C��D��E����ͬһ��ƽ���ڣ�����DE��4�ף��Ҵ�ʱ̫������ˮƽ���������Ϊ24������AED��24�������������¥AB�ĸߣ������У�sin24���0.41��cos24���0.91��tan24���0.45��
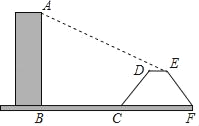
���𰸡�21.5�ף�
��������
�ӳ�ED��AB��G����DH��BF��H���ɵ��ı��� DHBG�Ǿ��Σ��Ӷ���DG��BH��DH��BG���ٸ���������ֱ����DCH��ֱ����AEG����������.
�⣺�ӳ�ED��AB��G����DH��BF��H��
��DE��BF��
���ı��� DHBG�Ǿ��Σ�
��DG��BH��DH��BG��
��![]() ��
��![]() ��CD��10��
��CD��10��
��DH��8��CH��6��
��GE��20+4+6��30��
��tan24����![]() ��0.45��
��0.45��
��AG��13.5��
��AB��AG+BG��13.5+8��21.5��
�𣺴�¥AB�ĸ�Ϊ21.5�ף�


��ϰ��ϵ�д�
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
�����Ŀ