题目内容
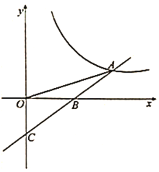
【题目】如图,AB、CD是⊙O的两条互相垂直的直径,E是![]() 上一点,连接AE,作OG∥AE交CE于点G.
上一点,连接AE,作OG∥AE交CE于点G.
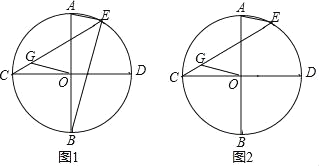
(1)求证:BE=![]() EG;
EG;
(2)判断AE与CG的数量关系,并证明.
【答案】(1)证明见解析;
(2)![]() .
.
【解析】
作OH⊥OG,交CE于H,连接AH,先证明△COG≌△AOH(SAS),可得出CG=AH和∠AHO=∠CGO=135°,得出![]() ,再由AB、CD是⊙O的两条互相垂直的直径得出
,再由AB、CD是⊙O的两条互相垂直的直径得出![]() ,进而证的△BCG∽△BAE,得出∠CEB=45°,从而证的△BGE三等腰直角三角形,即可得出BE=
,进而证的△BCG∽△BAE,得出∠CEB=45°,从而证的△BGE三等腰直角三角形,即可得出BE=![]() EG.
EG.
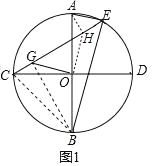
(1)如图1,证明:作OH⊥OG,交CE于H,连接AH,
∵OG∥AE,
∴∠OGH=∠AEC=45°,
∴∠OHG=45°,
∴OG=OH,
又∵∠COG=∠AOH=90°﹣∠AOG,OC=OA,
∴△COG≌△AOH(SAS),
∴CG=AH,∠AHO=∠CGO=135°,
∴∠AHC=90°,
∴AE=![]() AH=
AH=![]() CG,
CG,
∴![]() ,
,
∵AB、CD是⊙O的两条互相垂直的直径,
∴OC=OB=![]() AB,
AB,
连接BC,BG,
∴![]() ,
,
∴![]() ,
,
∵∠BCG=∠BAE,
∴△BCG∽△BAE,
∴∠CGB=∠AEB=90°,
∵∠CEB=45°,
∴△BGE三等腰直角三角形,
∴BE=![]() EG;
EG;
(2)解:作OH⊥OG,交CE于H,连接AH,
∵OG∥AE,
∴∠OGH=∠AEC=45°,
∴∠OHG=45°,
∴OG=OH,
又∵∠COG=∠AOH=90°﹣∠AOG,OC=OA,
∴△COG≌△AOH(SAS),
∴CG=AH,∠AHO=∠CGO=135°,
∴∠AHC=90°,
∴AE=![]() AH=
AH=![]() CG,
CG,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目