Question

【题目】数学中，把长与宽之比为（或宽与长之比为）的矩形称为黄金矩形.

思考解决下列问题：

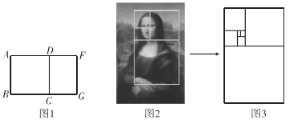
（1）已知图1中黄金矩形的长，求的长；

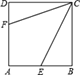
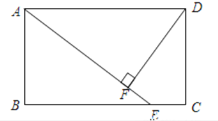
（2）黄金矩形有个奇妙的特性：把图1中的黄金矩形，以为边向矩形内作正方形，则矩形是否为黄金矩形，是，请予以证明；不是，请说明理由；

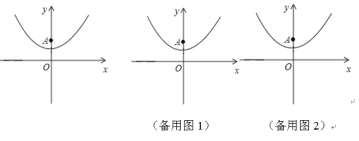
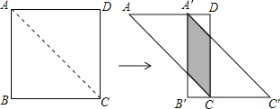
（3）黄金矩形使名画《蒙娜丽莎》显得特别和谐，专家分析画中布局如图2，其中最外面的矩形是黄金矩形，以黄金矩形的宽为边向矩形内部作正方形，由上小题知产生的小矩形为更小的黄金矩形，按此规律依次生成各黄金矩形，若图3中最大黄金矩形的长为，则最小黄金矩形的长是多少？

Answer 1

【答案】（1）；（2）矩形DCGF是黄金矩形，理由见解析；（3）.

【解析】

（1）根据黄金分割的定义代入求解即可；

（2）由正方形的性质得到点D为线段AF的黄金分割点，再根据黄金分割的定义判断即可；

（3）根据黄金分割的定义解答即可.

（1）由题意可得，，

∵，∴，即的长为.

（2）矩形是黄金矩形，理由如下：

∵四边形ABEF是正方形，∴AB=DC=AD，

又∵，∴,

即点D是线段AF的黄金分割点，

∴，∴，

∴矩形DCGF是黄金矩形．

（3）若图3中最大黄金矩形的长为a，由题意可得，

最小黄金矩形的长是.