题目内容
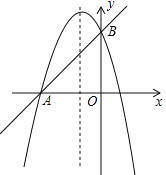
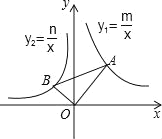
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )
A.m=![]() nB.m=﹣
nB.m=﹣![]() nC.m=﹣
nC.m=﹣![]() nD.m=﹣3n
nD.m=﹣3n
【答案】D
【解析】
过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,设点B坐标为(a,![]() ),点A的坐标为(b,
),点A的坐标为(b,![]() ),证明△BOE∽△OAF,利用对应边成比例可求出m、n的关系.
),证明△BOE∽△OAF,利用对应边成比例可求出m、n的关系.
过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,
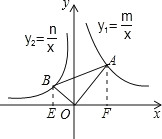
∵∠OAB=30°,
∴OA=![]() ,
,
设点B坐标为(a, ![]() ),点A的坐标为(b,
),点A的坐标为(b, ![]() ),
),
则OE=a,BE=![]() ,OF=b,AF=
,OF=b,AF=![]() ,
,
∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°,
∴∠OBE=∠AOF,
又∵∠BEO=∠OFA=90°,
∴△BOE∽△OAF,
∴![]() ,即
,即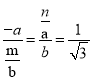 ,
,
解得:m![]() ,n=
,n=![]() ,
,
故可得:m=3n.
故选:D.

练习册系列答案
相关题目