题目内容
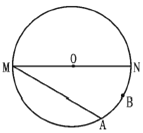
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点.
的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
【答案】(1)作图见解析;(2)2![]() .
.
【解析】试题分析:(1)画出A点关于MN的称点A′,连接A′B,就可以得到P点;
(2)利用∠AMN=30°得∠AON=∠A′ON=60°,又B为弧AN的中点,∴∠BON=30°,所以∠A′OB=90°,再求最小值2![]() .
.
试题解析:
(1)如图,点P即为所求作的点.

(2)由(1)可知,PA+PB的最小值为 A′B的长,
连接OA′,OB、OA,
∵A点关于MN的称点A′,∠AMN=30°,
∴∠AON=∠A′ON=2∠AMN=60°,
又∵B为![]() 的中点
的中点
∴![]() ,
,
∴∠BON=∠AOB=![]() ∠AON=30°,
∠AON=30°,
∴∠A′OB=∠A′ON+∠BON=60°+30°=90°,
又∵MN=4,
∴ OA′=OB=![]() MN=2,
MN=2,
在Rt△A′OB中,A′B=![]() =2
=2![]() ,
,
即PA+PB的最小值为2![]() .
.


练习册系列答案
相关题目



