题目内容
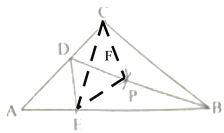
【题目】如图，在△ABC中，小刚同学按如下步骤作图：
(1)以B为圆心，BC长为半径画弧，交AB于点E
(2)分别以点C.E为圆心，大于
CE的长为半径画弧，两弧在△ABC内相交于点P
(3)连接BP,并延长交AC于点D
(4)连接DE
根据以上作图步骤，有下列结论：①BD平分∠ABC； ②AD+DE = AC；③点P与点D关于直线CE对称； ④△BCD与△BED关于直线BD对称.
其中正确结论的个数是（ ）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据作法（1）（2）可证△BCP≌△BEP，可判断BD是∠ABC的平分线，可证①②④都是正确的，因为CP是任意长，故无法证明点P与点D关于直线CE对称.
连接PC、PE
由作法（1）（2）得：
AC=AE，CP=CE，BP=BP
∴△BCP≌△BEP（SSS）
∴∠CBD=∠ABD
∴BD平分∠ABC，故①正确；
又∵BC=BE，∠CBD=∠ABD，BD=BD
∴△BCD≌△BED（SAS）
∴CD=DE
∴AD+DE = AD+CD=AC，故②正确；
连接CE，交BD于F点
∵BC=BE，∠CBD=∠ABD
∴BD垂直平分CE，故△BCD与△BED关于直线BD对称，故④正确；
∵CP是任意长，故无法证明点P与点D关于直线CE对称，故③错误.
故选：C
练习册系列答案
相关题目
