题目内容
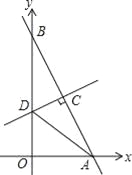
【题目】如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x﹣4)+8(4﹣x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
(1)求线段AB的长;
(2)求tan∠DAO的值;
(3)若把△ADC绕点A顺时针旋转α°(0<α<90),点D,C的对应点分别为D1,C1,得到△AD1C1,当AC1∥y轴时,分别求出点C1,点D1的坐标.
【答案】(1)、4![]() ;(2)、
;(2)、![]() ;(3)、C1(4,2
;(3)、C1(4,2![]() ),D1(4-
),D1(4-![]() ,2
,2![]() )
)
【解析】试题分析:(1)先根据方程的解求得线段OA,OB的长,再根据勾股定理求得AB的长;(2)先根据线段垂直平分线的性质,得到AD=BD,再根据Rt△AOD中的勾股定理,求得OD的长,并计算tan∠DAO的值;(3)先根据旋转的性质,求得AC1和C1D1的长,再根据OA=4,AC1∥y轴,求得点C1和点D1的坐标.
试题解析:(1)由方程x(x﹣4)+8(4﹣x)=0,解得
x1=4,x2=8,
即OA=4,OB=8,
∴由勾股定理可得AB=![]()
(2)∵CD为AB的垂直平分线,
∴AD=BD
∵在Rt△AOD中,OD2+OA2=AD2
即OD2+42=(8﹣OD)2,
∴OD=3
∴![]()
(3)由旋转可得,AC1=AC=2![]() ,C1D1=CD=
,C1D1=CD=![]() =
=![]()
又∵OA=4,AC1∥y轴
∴C1(4,2![]() ),D1(4-
),D1(4-![]() ,2
,2![]() )
)

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目