题目内容
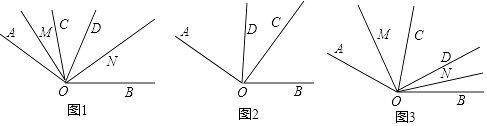
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 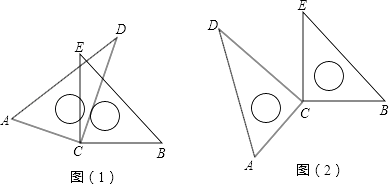
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
【答案】
(1)解:∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD
(2)解:若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°
(3)解:猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°
(4)解:成立
【解析】(1)根据余角的性质,可得答案;(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;(3)根据角的和差,可得答案;(4)根据角的和差,可得答案.
【考点精析】关于本题考查的余角和补角的特征,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关才能得出正确答案.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目