题目内容
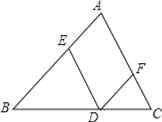
【题目】已知D为△ABC边BC上的一个动点（不与B，C重合），过D作DE∥AC交AB于点E，作DF∥AB交AC于点F．
（1）证明：△BDE∽△DCF；
（2）若△ABC的面积为10，点G为线段AF上的任意一点，设FC：AC=n，△DEG的面积为S，求S关于n的关系式，并求S的最大值．
【答案】(1)、证明过程见解析；(2)、S=﹣10n2+10n；最大值2.5
【解析】试题分析：（1）根据相似三角形的判定证明即可；（2）根据相似三角形的性质和二次函数的最值解答即可．
试题解析：（1）∵DF∥AB，
∴△DFC∽△BAC，
∵DE∥AC，
∴△BED∽△BAC
∴△DFC∽△BED；
（2）∵△BED∽△DFC∽△BAC，FC：AC=n，△ABC的面积为10，
∴
，
，
，
，
，
∵点G为线段AF上的任意一点，
，
∴S=﹣10n2+10n=﹣10
，
∴S的最大值是2.5．
练习册系列答案
相关题目
