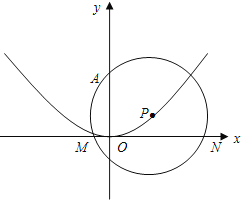��Ŀ����
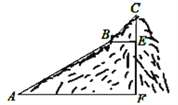
����Ŀ����ͼ1������ABC�͡�ADEΪ�ȱ������Σ�M��N�ֱ�EB��CD���е㣬��֤��CD=BE����AMN�ǵȱ������Σ�
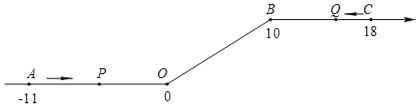
(1)���ѡ�ADE��A����ת��ͼ2��λ��ʱ��CD=BE�Ƿ���Ȼ��������������֤��������������˵�����ɣ�
(2)����ADE��A����ת��ͼ3��λ��ʱ����AMN�Ƿ��ǵȱ������Σ����������֤����
(3)��(2)�������£������AB=2ADʱ����ADE���ABC����AMN�����֮��S��ADE��S��ABC�� S��AMN��

���𰸡���1��(1)CD=BE�����ɼ���������2����AMN�ǵȱ������Σ����ɼ���������3��4:16:7
�������������������1����������SAS�ж���ABE�ա�ACD��Ȼ�����ȫ�������εĶ�Ӧ����ȣ��õ�CD=BE����2������֤����AMN�ǵȱ������Σ�AD=a����AB=2a����AB=2a����3��������֪�����ֱ������AMN�ı߳�����Ϊ��ADE����ABC����AMNΪ�ȱ������Σ���������ȵ��ڱ߳���ƽ���ıȣ��ݴ˽�ɣ�
(1)CD=BE���������£���
�ߡ�ABC����ADEΪ�ȱ������Σ�
��AB=AC��AE=AD����BAC=��EAD=60o��
�ߡ�BAE =��BAC����EAC =60o����EAC��
��DAC =��DAE����EAC =60o����EAC��
���BAE=��DAC��
���ABE �� ��ACD��
��CD=BE��
(2)��AMN�ǵȱ������Σ��������£�
�ߡ�ABE �� ��ACD��
���ABE=��ACD��
��M��N�ֱ���BE��CD���е㣬
��BM= ![]() ��
��
��AB=AC����ABE=��ACD��
���ABM �� ��ACN��
��AM=AN����MAB=��NAC��
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60o��
���AMN�ǵȱ������Σ�
(3) ��AD=a����AB=2a��
��AD=AE=DE��AB=AC��
��CE=DE��
�ߡ�ADEΪ�ȱ������Σ�
���DEC=120 o�� ��ADE=60o��
���EDC=��ECD=30o��
���ADC=90o.
����Rt��ADC��AD=a����ACD=30 o ��
�� CD= ![]() ��
��
��NΪDC�е㣬
��![]() ��
��
�� ��
��
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC�� S��AMN=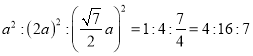

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�