题目内容
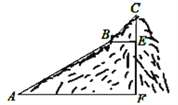
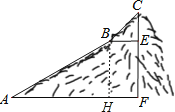
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.求山峰的高度CF(结果保留根号)
【答案】山峰的高度是(300+100![]() )米
)米
【解析】试题分析:作BH⊥AF于H,如图,在Rt△ABH中根据正弦的定义可计算出BH的长,从而得到EF的长;再在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
试题解析:(1)作BH⊥AF于H,如图,
在Rt△ABH中,∵sin∠BAH=![]() ,
,
∴BH=600sin30°=300,
∴EF=BH=300m;
(2)在Rt△CBE中,∵sin∠CBE=![]() ,
,
∴CE=200sin45°=100![]() ,
,
∴CF=EF+CE=(300+100![]() )m.
)m.
答:山CF的高度约为(300+100![]() )米.
)米.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目