Question

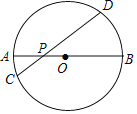
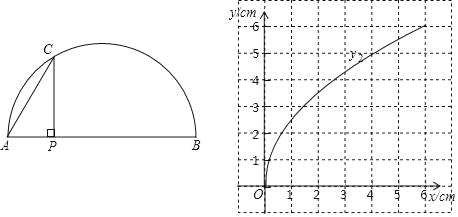
【题目】在如图所示的半圆中，P是直径AB上一动点，过点P作PC⊥AB于点P，交半圆于点C，连接AC．已知AB＝6cm，设A，P两点间的距离为xcm，P，C两点间的距离为cm，A，C两点间的距离为cm．

小聪根据学习函数的经验，分别对函数，随自变量x的变化而变化的规律进行了探究．

下面是小聪的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了，与x的几组对应值；

/tr>

x/cm	0	1	2	3	4	5	6
y1/cm	0	2.24	2.83		2.83	2.24	0
y2/cm	0	2.45	3.46	4.24	4.90	5.48	6

（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，），（x，），并画出函数，的图象；

（3）结合函数图象，解决问题：当△APC有一个角是30°时，AP的长度约为______cm．

Answer 1

【答案】（1）x＝3时，y1＝3；（2）见解析；（3）1.5或4.5

【解析】

(1) 由PC＝3时，PA＝PB＝3，可得PC＝3cm，即y1＝3；

(2)利用描点法画出函数图象即可;

(3)当∠ACP＝30°时，可得AP＝1.50cm，根据对称性，结合图象可知：当∠CAP＝30°时，PB＝1.50cm，PA＝4.50cm．

解：（1）因为PC＝3时，PA＝PB＝3，

∴PC是⊙O的半径，

∴PC＝3cm，即x＝3时，y1＝3．

（2）利用描点法画出函数图象即可．

（3）结合图象可知：当∠ACP＝30°时，AP＝AC，由图像得，此时x=1.5，即AP＝1.50cm．

根据对称性，结合图象可知：当∠CAP＝30°时，PC＝AC，AP＝4.50cm．