��Ŀ����
����Ŀ��֪ʶ��������������30��ǵ�ȫ�����dz߷���һ����������30���Ǻ���һ���60��������ƴ�ա��۲졢˼����̽������ֱ����������30������Ե�ֱ�DZߵ���б�ߵ�һ�롱������
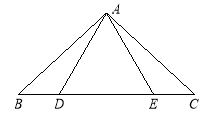
��ͼ���ȱ�������ABC�ı߳�Ϊ4cm����D�ӵ�C������CA��A�˶�����E��B������AB���ӳ���BF�����˶�����֪��D��E����ÿ��0.5cm���ٶ�ͬʱ��ʼ�˶����˶�������DE��BC�ཻ�ڵ�P�����˶�ʱ��Ϊx����
��1����ֱ��д��AD��������x�Ĵ���ʽ��ʾ��
��2������ADEΪֱ��������ʱ���˶�ʱ��Ϊ���룿
��2����֤�����˶�����������Pʼ��Ϊ�߶�DE���е���
���𰸡���1��AD=4-0.5x����2��![]() ����3��֤����������
����3��֤����������
�������������������1��ֱ�Ӹ���AD=AC-CD�������2����x��ʱ����ADEΪֱ�������Σ��ֱ��ú�x��ʽ�ӱ�ʾ��AD��AE���ٸ���Rt��ADE��30������Ե�ֱ�DZߵ���б�ߵ�һ��ó�x�ķ��̣���⼴�ɣ���3����DG��AB��BC�ڵ�G��֤��DGP�ա�EBP��ɵ�.
�⣺��1����AC=4��CD=0.5x����AD=AC-CD=4-0.5x��
��2���ߡ�ABC�ǵȱ������Σ�
��AB=BC=AC=4cm����A=��ABC=��C=60�㣮
��x��ʱ����ADEΪֱ�������Σ�
���ADE=90�㣬CD=0.5x��BE=0.5x��AD=4-0.5x��AE=4+0.5x��
���AED=30�㣬��AE=2AD��
��4+0.5x=2��4-0.5x������x=![]() .
.
���˶�![]() �����ADEΪֱ�������Σ�
�����ADEΪֱ�������Σ�
��3����DG��AB��BC�ڵ�G��
���GDP=��BEP����CDG=��A=60�㣬��CGD=��ABC=60�㣬
���C=��CDG=��CGD��
���CDG�ǵȱ������Σ���DG=DC��
��DC=BE����DG=BE��
����DEP����EBP������GDP��BEP����DPG����EPB��DG��EB��
���DGP�ա�EBP����DP=PE��
�����˶������У���Pʼ��Ϊ�߶�DE���е㣮