题目内容
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销![]() 件.已知产销两种产品的有关信息如下表:
件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(件) |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中![]() 为常数,且
为常数,且![]() .
.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与
与![]() 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【答案】(1)![]() (
(![]() ),
),![]() (
(![]() );(2)产销甲种产品的最大利润为
);(2)产销甲种产品的最大利润为![]() 万元,产销乙种产品的最大年利润为440万元;(3)当
万元,产销乙种产品的最大年利润为440万元;(3)当![]() 时,生产甲产品的利润高;当
时,生产甲产品的利润高;当![]() 时,生产甲乙两种产品的利润相同;当
时,生产甲乙两种产品的利润相同;当![]() 时,生产乙产品的利润高.理由见解析
时,生产乙产品的利润高.理由见解析
【解析】
(1)根据利润=销售数量×每件的利润即可解决问题;
(2)根据一次函数的增减性,二次函数的增减性即可解决问题;
(3)根据题意分三种情形分别求解即可:①(1180200a>440,②(1180200a)=440,③(1180200a)<440.
(1)![]() (
(![]() ),
),
![]() (
(![]() )
)
(2)甲产品:∵![]() ,∴
,∴![]() ,∴
,∴![]() 随
随![]() 的增大而增大.
的增大而增大.
∴当![]() 时,
时,![]() (
(![]() )
)
乙产品:![]() =-0.05(x-100)2+460(
=-0.05(x-100)2+460(![]() )
)
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
当![]() 时,
时,![]() (万元).
(万元).
∴产销甲种产品的最大利润为![]() 万元,产销乙种产品的最大年利润为440万元;
万元,产销乙种产品的最大年利润为440万元;
(3)![]() ,解得
,解得![]() 时,此时选择甲产品;
时,此时选择甲产品;
![]() ,解得
,解得![]() 时,此时选择甲乙产品;
时,此时选择甲乙产品;
![]() ,解得
,解得![]() 时,此时选择乙产品.
时,此时选择乙产品.
∴当![]() 时,生产甲产品的利润高;
时,生产甲产品的利润高;
当![]() 时,生产甲乙两种产品的利润相同;
时,生产甲乙两种产品的利润相同;
当![]() 时,生产乙产品的利润高.
时,生产乙产品的利润高.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
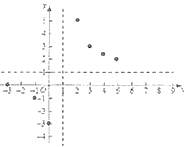
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.