题目内容
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )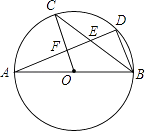
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
【答案】D
【解析】解:①、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,③、∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,④、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,⑤、由④有,AF=DF,
∵点O为AB中点,
∴OF是△ABD的中位线,
∴BD=2OF,⑥∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故答案为:D
①、根据AB是⊙O的直径得出结论;② 在△AOF和△CFE中,由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,,可知∠AOC≠∠AEC;③、根据同圆的半径相等及平行线的性质可以得出结论;④由垂径定理得出结论;⑤由中位线定理可得出结论;⑥△CEF和△BED中,没有相等的边故得不出结论。

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
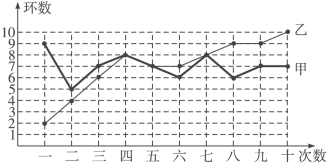
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
【题目】当自然数![]() 的个位数分别为0,1,2,…,9时,
的个位数分别为0,1,2,…,9时,![]() 的个位数如表所示:
的个位数如表所示:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
| 0 | 1 | 8 | 7 | 4 | 5 | 6 | 3 | 2 | 9 |
| 0 | 1 | 6 | 1 | 6 | 5 | 6 | 1 | 6 | 1 |
······ |
在10,11,12,13这四个数中,当![]() ____________时,和数
____________时,和数![]() 能被5整除.
能被5整除.