题目内容
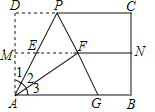
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

【答案】35
【解析】
根据题意知,阴影部分的面积等于两个正方形的面积减去两个三角形的面积,由给出的条件即可求出阴影部分的面积.
∵AP=a,BP=b
∴正方形APCD的面积S1= a2 正方形PBEF的面积S2=b2
∵点M是AB的中点
∴AM=MB=![]() AB=
AB=![]() (a+b)
(a+b)
∴S△ADM=![]() AM×DA=
AM×DA=![]() ×
×![]() (a+b) ×a=
(a+b) ×a=![]() (a2+ab)
(a2+ab)
S△MBE=![]() MB×BE=
MB×BE=![]() ×
×![]() (a+b) ×b=
(a+b) ×b=![]() (b2+ab)
(b2+ab)
∴S阴影= S1+ S2- S△ADM- S△MBE
= a2+ b2-![]() (a2+ab)-
(a2+ab)-![]() (b2+ab)
(b2+ab)
=![]() a2+
a2+![]() b2-
b2-![]() ab
ab
=![]() (a+b)2-2ab
(a+b)2-2ab
=![]() ×102-2×20
×102-2×20
=75-40
=35.
故答案为:35.

练习册系列答案
相关题目