题目内容
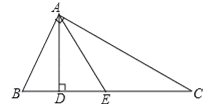
【题目】如图,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.求:
(1)△ABC的面积;
(2)AD的长;
(3)△ACE和△ABE的周长的差.
【答案】(1)24;(2)4.8;(3)2.
【解析】试题分析:(1)根据三角形的面积公式计算即可;
(2)利用“面积法”来求线段AD的长度;
(3)由于AE是中线,那么BE=CE,于是△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE),化简可得△ACE的周长﹣△ABE的周长=AC﹣AB,易求其值.
解:(1)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=![]() ABAC=
ABAC=![]() ×6×8=24(cm2).
×6×8=24(cm2).
(2)∵∠BAC=90°,AD是边BC上的高,
∴![]() ABAC=
ABAC=![]() BCAD,
BCAD,
∴AD=![]() (cm),
(cm),
即AD的长度为4.8cm;

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目