题目内容
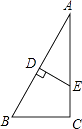
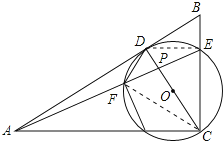
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

【答案】(1))AB是⊙O切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得![]() ,设PF=a.则PC=2a,列出方程即可解决问题.
,设PF=a.则PC=2a,列出方程即可解决问题.
试题解析:(1)AB是⊙O切线.
理由:连接DE、CF.
∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴![]() ,
,
∴PC2=PFPA,设PF=a.则PC=2a,
∴4a2=a(a+5),
∴a=![]() ,
,
∴PC=2a=![]() .
.

练习册系列答案
相关题目