题目内容
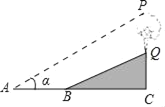
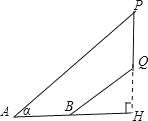
【题目】如图,已知斜坡BQ的坡度i=1:2.4,坡长BQ=13米,在斜坡BQ上有一棵银杏树PQ,小李在A处测得树顶P的仰角为α,测得水平距离AB=8米.若tanα=0.75,点A,B,P,Q在同一平面上,PQ⊥AB于点C,则银杏树PQ的高度为_____米.
【答案】10
【解析】
先延长PQ交直线AB于点H,得直角三角形QBH,根据坡度为i=1:2.4和勾股定理求出QH和BH,从而得出AH,再由直角三角形和tanα=0.75求出PH,继而求出银杏树PQ的高度进行解答即可.
解:延长PQ交直线AB于点H.
∵在Rt△QBH中,QH:BH=1:2.4.
∴设QH=x,BH=2.4x,
∵BQ=13米,
∴x2+(2.4x)2=132.
∴x=±5(负值舍去).
∴QH=5(米),BH=12(米).
∵AB=8(米),
∴AH=20(米).
∵tanα=0.75,
∴![]() .
.
即![]() ,
,
∴PH=15(米).
∴PQ=PH﹣QH=15﹣5=10(米)

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目