题目内容
【题目】如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.
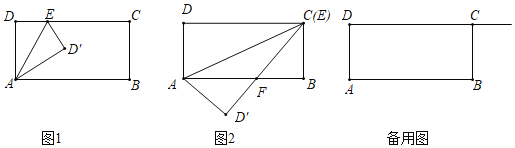
(1)当D′点落在AB边上时,∠DAE= °;
(2)如图2,当E点与C点重合时,D′C与AB交点F,
①求证:AF=FC;②求AF长.
(3)连接D′B,当∠AD′B=90°时,求DE的长.
【答案】(1)45;(2)①见解析;②AF=6.8;(3)DE=2或18.
【解析】
(1)由△ADE≌△AD′E知∠DAE=∠D′AE,结合D′点落在AB边上知∠DAE+∠D′AE=90°,从而得出答案;
(2)①由折叠得出∠ACD=∠ACD′,再由AB∥CD得出∠ACD=∠BAC,从而得知∠ACD′=∠BAC,据此即可得证;
②设AF=FC=x,则BF=10﹣x,在Rt△BCF中,由BF2+BC2=CF2得到关于x的方程,解之可得;
(3)分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
解:(1)由题意知△ADE≌△AD′E,
∴∠DAE=∠D′AE,
∵D′点落在AB边上时,∠DAE+∠D′AE=90°,
∴∠DAE=∠D′AE=45°,
故答案为:45;
(2)①如图2,由题意知∠ACD=∠ACD′,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠ACD=∠BAC,
∴∠ACD′=∠BAC,
∴AF=FC;
②设AF=FC=x,则BF=10﹣x,
在Rt△BCF中,由BF2+BC2=CF2得(10﹣x)2+62=x2,
解得x=6.8,即AF=6.8;
(3)如图3,
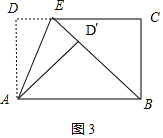
∵△AD′E≌△ADE,
∴∠AD′E=∠D=90°,
∵∠AD′B=90°,
∴B、D′、E三点共线,
又∵△ABD′∽△BEC,AD′=BC,
∴△ABD′≌△BEC,
∴BE=AB=10,
∵BD′=![]() =
=![]() =8,
=8,
∴DE=D′E=10﹣8=2;
如图4,
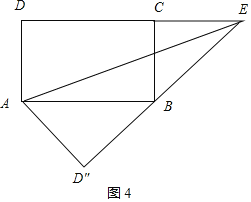
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵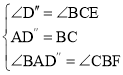 ,
,
∴△ABD″≌△BEC,
∴BE=AB=10,
∴DE=D″E=8+10=18.
综上所知,DE=2或18.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某电子超市销售甲、乙两种型号的蓝牙音箱,每台进价分别为240元,140元,下表是近两周的销售情况:(销售收入=销售单价×销售数量)
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 3台 | 7台 | 2160元 |
第二周 | 5台 | 14台 | 4020元 |
求甲、乙两种型号蓝牙音箱的销售单价.
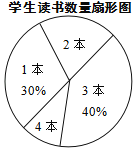
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?