题目内容
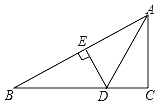
【题目】如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转
得到线段PE，连接AE，BP，CE.
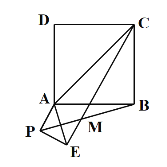
（1）求证：
；
（2）当线段BP与CE相交时，设交点为M，求
的值以及
的度数；
（3）若正方形ABCD的边长为3，
，当点P，C，E在同一直线上时，求线段BP的长.
【答案】（1）见解析；（2）
，
；（3）
或
【解析】
（1）根据题意可知
为等腰直角三角形，根据等腰直角三角形性质和正方形的性质可得
，
，然后利用两组对应边成比例及其夹角相等的两个三角形相似即可证出
；
（2）利用两组对应边成比例及其夹角相等的两个三角形相似，即可证出
，利用相似三角形的性质即可求出
的值，
，然后利用三角形的内角和即可求出
；
（3）根据点P、C、E的相对位置分类讨论：①当点E在线段CP上时，利用勾股定理求出PC的长，从而求出CE的长，再根据（2）的结论即可求出BP；②当点P在线段CE上时，原理同上.
解：（1）∵线段AP绕点P顺时针旋转
得到线段PE
∴为等腰直角三角形
∴
，
∵在正方形ABCD中，
，
∴，
∴
∴
（2）由（1）知
∴
即
又∵
∴
∴
，
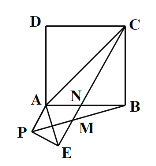
又∵
∴
（3）①如下图所示，当点E在线段CP上时
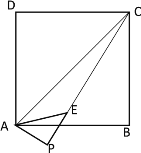
∵在正方形ABCD中，∠
，
∴
∴在
中，
∴
∵由（2）知
且
∴；
②如下图所示，当点P在线段CE上时
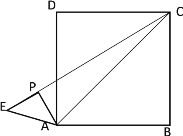
由①得，
∴
由（2）知且
∴
；
综上所述：或.
练习册系列答案
相关题目
