题目内容
【题目】已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三边的距离之和为（ ）
A.
B.
C.
D.不能确定
【答案】B
【解析】解：如图，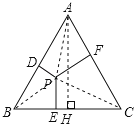
∵等边三角形的边长为3，
∴高线AH=3× 
= 
，S△ABC= 
BCAH= ABPD+ BCPE+ ACPF，
∴ ×3AH= ×3PD+ ×3PE+ ×3PF，
∴PD+PE+PF=AH= ，即点P到三角形三边距离之和为 ．
故选：B．
作出图形，根据等边三角形的性质求出高AH的长，再根据三角形的面积公式求出点P到三边的距离之和等于高线的长度，从而得解．本题考查了等边三角形的性质，根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论：
1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
2）当 
时，y＜0；
3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（ ）
A.3
B.2
C.1
D.0
