��Ŀ����
����Ŀ�����Ƕ��壺��һ���ڽ���ȵ��ı��ν��������ڽ��ı��Ρ�
��1���������⣺
����������������һ�����ڽ��ı��ε����ӣ�
��2������̽����
��ͼ1���ڵ��ڽ��ı���ABCD�У���DAB=��ABC��AD��BC���д���ǡ�ý���AB����һ��P������AC��BD����̽��AC��BD��������ϵ����˵�����ɣ�
��3��Ӧ����չ��
��ͼ2����Rt��ABC��Rt��ABD�У���C=��D=90�㣬BC=BD=3��AB=5����Rt��ABD���ŵ�A˳ʱ����ת�Ǧ���0�㣼�Ϧ�����BAC���õ�Rt��AB��D�䣨��ͼ3�������ı���AD��BCΪ���ڽ��ı���ʱ��������������
���𰸡�
��1��
���������
��2��
�⣺AC=BD������Ϊ��
����PD��PC����ͼ1��ʾ��

��PE��AD�Ĵ�ֱƽ���ߣ�PF��BC�Ĵ�ֱƽ���ߣ�
��PA=PD��PC=PB��
���PAD=��PDA����PBC=��PCB��
���DPB=2��PAD����APC=2��PBC������PAD=��PBC��
���APC=��DPB��
���APC�ա�DPB��SAS����
��AC=BD��
��3��
�⣺������������ǣ�
��i������AD��B=��D��BCʱ���ӳ�AD�䣬CB���ڵ�E��
��ͼ3��i����ʾ��

���ED��B=��EBD�䣬
��EB=ED�䣬
��EB=ED��=x��
�ɹ��ɶ����ã�42+��3+x��2=��4+x��2��
��ã�x=4.5��
����D����D��F��CE��F��
��D��F��AC��
���ED��F�ס�EAC��
�� ![]() ����
���� ![]() ��
��
��ã�D��F= ![]() ��
��
��S��ACE= ![]() AC��EC=
AC��EC= ![]() ��4����3+4.5��=15��S��BED��=
��4����3+4.5��=15��S��BED��= ![]() BE��D��F=
BE��D��F= ![]() ��4.5��
��4.5�� ![]() =
= ![]() ��
��
��S�ı���ACBD��=S��ACE��S��BED��=15�� ![]() =10
=10 ![]() ��
��
��ii������D��BC=��ACB=90��ʱ������D����D��E��AC�ڵ�E��
��ͼ3��ii����ʾ��
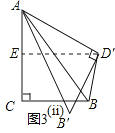
���ı���ECBD���Ǿ��Σ�
��ED��=BC=3��
��Rt��AED���У����ݹ��ɶ����ã�AE= ![]() =
= ![]() ��
��
��S��AED��= ![]() AE��ED��=
AE��ED��= ![]() ��
�� ![]() ��3=
��3= ![]() ��S����ECBD��=CE��CB=��4��
��S����ECBD��=CE��CB=��4�� ![]() ����3=12��3
����3=12��3 ![]() ��
��
��S�ı���ACBD��=S��AED��+S����ECBD��= ![]() +12��3
+12��3 ![]() =12��
=12�� ![]() ��
��
����������1�����λ��������ڽ���ȣ����㡰���ڽ��ı��Ρ���������2��AC=BD������Ϊ������PD��PC����ͼ1��ʾ������PE��PF�ֱ�ΪAD��BC�Ĵ�ֱƽ���ߣ��õ����Խ���ȣ����õȽǶԵȽǵõ����Խ���ȣ�����ȷ������APC=��DPB������SAS�õ�������ACB��������DPBȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤����3��������������ǣ���i������AD��B=��D��BCʱ���ӳ�AD�䣬CB���ڵ�E����ͼ3��i����ʾ����S�ı���ACBD��=S��ACE��S��BED�� �� ����ı���ACBD���������ii������D��BC=��ACB=90��ʱ������D����D��E��AC�ڵ�E����ͼ3��ii����ʾ����S�ı���ACBD��=S��AED��+S����ECBD�� �� ����ı���ACBD��������ɣ��������ڼ��α任�ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ����������ε��ж������ʣ���ֱƽ���߶������������������ʣ��Լ����ε��ж������ʣ����������ж��������ǽⱾ��Ĺؼ���
�����㾫����������Ŀ����֪���������õ��������ε����ʺ����������ε��ж������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����





