题目内容
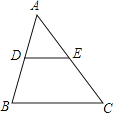
【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.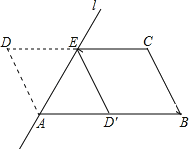
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.
【答案】
(1)
证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴CE=D′B,CE∥D′B,
∴四边形BCED′是平行四边形;
∵AD=AD′,
∴DAD′E是菱形
(2)
证明:∵四边形DAD′E是菱形,
∴D与D′关于AE对称,
连接BD交AE于P,则BD的长即为PD′+PB的最小值,
过D作DG⊥BA于G,
∵CD∥AB,
∴∠DAG=∠CDA=60°,
∵AD=1,
∴AG= ![]() ,DG=
,DG= ![]() ,
,
∴BG= ![]() ,
,
∴BD= ![]() =
= ![]() ,
,
∴PD′+PB的最小值为 ![]() .
.

【解析】(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG= ![]() ,DG=
,DG= ![]() ,根据勾股定理即可得到结论.本题考查了平行四边形的性质,最短距离问题,勾股定理,菱形的判定和性质,正确的作出辅助线是解题的关键.
,根据勾股定理即可得到结论.本题考查了平行四边形的性质,最短距离问题,勾股定理,菱形的判定和性质,正确的作出辅助线是解题的关键.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形)的相关知识才是答题的关键.

【题目】如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
人数 | a | 12 | 36 | 18 | b |

解答下列问题:
(1)本次调查中的样本容量是;
(2)a= , b=;
(3)试估计上述1000名学生中最喜欢羽毛球运动的人数.
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD、FH.
【题目】为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
组别 | 分组 | 频数(人数) | 频率 |
1 | 10≤t<30 | ① | 0.16 |
2 | 30≤t<50 | 20 | ② |
3 | 50≤t<70 | ③ | 0.28 |
4 | 70≤t<90 | 6 | ④ |
5 | 90≤t<110 | ⑤ | ⑥ |
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?