题目内容
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
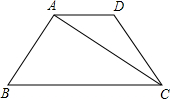

∵AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,
∴∠B=∠BCD=60°,∠ACB=∠ACD=∠CAD=30°
∴∠BAC=90°
设AB=CD=x,则AD=x,BC=2x.
所以x+x+x+2x=20,x=4.
AC=
AB=4
作AE⊥BC于E,则AE=
AC=2
.
则梯形的面积=
(4+8)×2
=12
.
即AC的长为4
,梯形面积为12
.
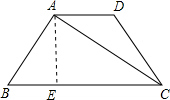
∴∠B=∠BCD=60°,∠ACB=∠ACD=∠CAD=30°
∴∠BAC=90°
设AB=CD=x,则AD=x,BC=2x.
所以x+x+x+2x=20,x=4.
AC=
| 3 |
| 3 |
作AE⊥BC于E,则AE=
| 1 |
| 2 |
| 3 |
则梯形的面积=
| 1 |
| 2 |
| 3 |
| 3 |
即AC的长为4
| 3 |
| 3 |


练习册系列答案
相关题目

 ,0),C(6,2
,0),C(6,2

