题目内容
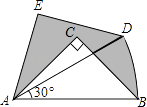
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 的中点,以
的中点,以![]() 为腰向外作等腰直角三角形
为腰向外作等腰直角三角形![]() ,
,![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() ,则
,则![]() .
.

【答案】(1) 20°; (2)见解析;(3)18.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
(1)∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°140°)÷2=20°;
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中, ![]() ,
,
∴△BAF≌△CAF(SAS).
∴∠ABF=∠ACF.
又∵AB=AC,
∴∠ABE=∠AEB,
∴∠AEB=∠ACF.
(3)
∵△BAF≌△CAF,
∴BF=CF.
∴∠AEB=∠ACF,∠AGE=∠FGC.
∴∠CFG=∠EAG=90°.
∴EF2+BF2=EF2+CF2=EC2.
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE.
∴EC2=AC2+AE2=2AC2=18.
即EF2+BF2=18.
故答案为:18.

练习册系列答案
相关题目