题目内容
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
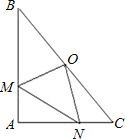
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
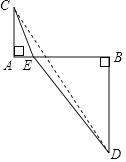
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
【答案】(1)①![]() ,
,![]() ;②
;②![]() ;(2)20.
;(2)20.
【解析】
(1)①利用勾股定理得到CE=![]() ,DE=
,DE=![]() ;
;
②根据CE+DE=![]() +
+![]() ,利用两点之间线段得到CE+DE≥CD(当且仅当C、E、D共线时取等号),作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,利用勾股定理计算出CD=
,利用两点之间线段得到CE+DE≥CD(当且仅当C、E、D共线时取等号),作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,利用勾股定理计算出CD=![]() ,从而求解;
,从而求解;
(2)如(1)中图,设AB=16,CA=5,BD=7,AE=x,则BE=16-x,利用勾股定理得到CE=![]() ,DE=
,DE=![]() ;根据两点之间线段得到而CE+DE≥CD(当且仅当C、E、D共线时取等号),根据四边形ABDH为矩形,利用勾股定理计算出CD即可得到最小值.
;根据两点之间线段得到而CE+DE≥CD(当且仅当C、E、D共线时取等号),根据四边形ABDH为矩形,利用勾股定理计算出CD即可得到最小值.
解:(1)①在Rt△ACE中,![]() ,
,
在Rt△BDE中,DE=![]() ;
;
②CE+DE=![]() +
+![]() ,
,
而CE+DE≥CD(当且仅当C、E、D共线时取等号),
作DH⊥CA交CA的延长线于H,如图,易得四边形ABDH为矩形,
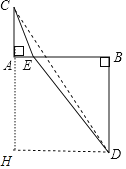
∴AH=BD=2,DH=AB=2,
在Rt△CHD中,CD=![]() ,
,
∴CE+DE的最小值为![]() ,即
,即![]() 的最小值为
的最小值为![]() ;
;
(2)如(1)中图,设AB=16,CA=5,BD=7,AE=x,则BE=16-x,
在Rt△ACE中,CE=![]() ,
,
在Rt△BDE中,DE=![]()
∴CE+DE=![]() +
+![]() ,
,
而CE+DE≥CD(当且仅当C、E、D共线时取等号),
∵四边形ABDH为矩形,
∴AH=BD=7,DH=AB=16,
在Rt△CHD中,CD=![]()
∴CE+DE的最小值为20,即![]() 的最小值为20.
的最小值为20.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4