Question

【题目】如图，PA、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交PA、PB于点E、F，已知PA=12cm，∠P=40°

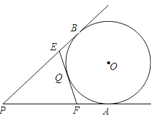
（1）求△PEF的周长.

（2）求∠EOF的度数.

Answer 1

【答案】（1）24cm；（2）70°.

【解析】

①根据切线长定理得出PA=PB，EB=EQ，FQ=FA，由PE+EF+PF=PE+EQ+FQ+PF即可求出答案．
②连接OE，OF，求出∠OEF+∠OFE的度数，即可得出∠EOF的度数．

（1）解：∵PA、PB是⊙O的切线，

∴PA=PB，

又∵直线EF是⊙O的切线，

∴EB=EQ，FQ=FA，

∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm

（2）解：

连接OE，OF，则OE平分∠BEF，OF平分∠AFE，

则∠OEF+∠OFE=（∠P+∠PFE）+∠（P+∠PEF）=（180°+40°）=110°，

∴∠EOF=180°﹣110°=70°．