题目内容
【题目】已知![]() 的三边长
的三边长![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都是整数,且
都是整数,且![]() ,
,![]() 的最大公约数为
的最大公约数为![]() .点
.点![]() 和点
和点![]() 分别为
分别为![]() 的重心和内心,且
的重心和内心,且![]() .则
.则![]() 的周长为________.
的周长为________.
【答案】![]()
【解析】
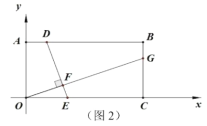
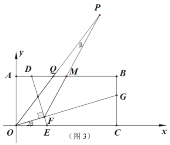
延长GI分别交BC于点P,AC于点Q,首先证明△CPQ为等腰三角形,根据内心和重心的知识分别表示出△PCQ的面积,进而求出a,b,c之间的等量关系式,最后对a,b,c进行讨论,进而求出a,b和c的值.
延长GI分别交BC于点P,AC于点Q,

∵∠GIC=90°,
∴GI⊥CI,I是内心,
∴△CPQ为等腰三角形,
∴PC=QC,
∴S△PCQ=2S△CQI=r×CQ(r为三角形ABC内切圆半径)
∴S△PCQ=S△PGC+S△CGQ=![]() PCha(ha为GE⊥BC的高)+
PCha(ha为GE⊥BC的高)+![]() CQhb(hb为GF⊥AC的高)=
CQhb(hb为GF⊥AC的高)=![]() CQ(ha+hb)=r×CQ,
CQ(ha+hb)=r×CQ,
∴2r=ha+hb①,
∵r=![]() ②,
②,
∵S△ABC=![]() ×aha'(ha'为AM⊥BC的高)=
×aha'(ha'为AM⊥BC的高)=![]() ×aha,
×aha,
∴ha=![]() ,hb=
,hb=![]() ,
,
∴ha+hb=![]() +
+![]() ③,
③,
把②③代入①得![]() ,
,
当a=2,b=2时,c=2,
∵△ABC为等边三角形,
∴GI重合,舍去,
∴a≠b,
设a>b,a=2m,b=2n,
∵a、b的最大公约数为2,
∴(m,n)=1,
∴m+n整除12,
即m=7,n=5,
∴a=14,b=10,c=11,
∴a+b+c=35.
故答案为:35

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目