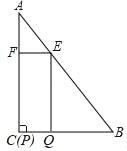
题目内容
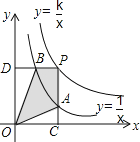
【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④S阴影=
CE;④S阴影=![]() .其中正确的个数为( )
.其中正确的个数为( )
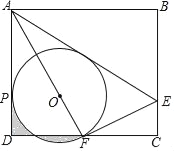
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①易求得DF长度,即可判定;
②连接OP,易证OP∥CD,根据平行线性质即可判定;
③易证AE=2EF,EF=2EC即可判定;
④连接OG,作OH⊥FG,易证△OFG为等边△,即可求得S阴影即可解题.
①∵AF是AB翻折而来,
∴AF=AB=6,
∵四边形ABCD是矩形,
AD=BC=3![]() ,
,
∴DF=![]() =
=![]() =3,
=3,
∴F是CD中点;
∴①正确;
②连接OP,
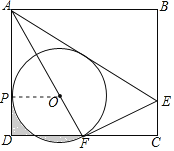
∵⊙O与AD相切于点P,
∴OP⊥AD,
∵AD⊥DC,
∴OP∥CD,
∴![]() ,
,
设OP=OF=x,则![]() ,
,
解得:x=2,
∴②正确;
③∵Rt△ADF中,AF=6,DF=3,
∴∠DAF=30°,∠AFD=60°,
∴∠EAF=∠EAB=30°,
∴AE=2EF;
∵∠AFE=90°,
∴∠EFC=90°-∠AFD=30°,
∴EF=2EC,
∴AE=4CE,
∴③错误;
④连接OG,作OH⊥FG,
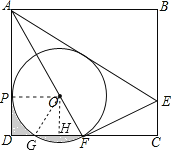
∵∠AFD=60°,OF=OG,
∴△OFG为等边三角形;同理△OPG为等边三角形;
∴∠POG=∠FOG=60°,OH=![]() ,S扇形OPG=S扇形OGF,
,S扇形OPG=S扇形OGF,
∴S阴影=(S矩形OPDH-S扇形OPG-S△OGH)+(S扇形OGF-S△OFG)=S矩形OPDH-![]() S△OFG=2×
S△OFG=2×![]() -
-![]() ×
×![]() ×2×
×2×![]() =
=![]() .
.
∴④正确;
其中正确的结论有:①②④,3个;
故选:C.

练习册系列答案
相关题目