Question

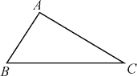
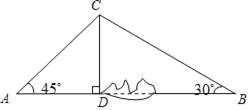
【题目】如图，为加快城乡对接，建设全域美丽乡村，某地区对A，B两地间的公路进行改建．如图，A，B两地之间有一座山，汽车原来从A地到B地需途径C地沿折线ACB行驶，现开通隧道后，汽车可直接沿直线AB行驶．已知BC＝80千米，∠A＝45°，∠B＝30°，开通隧道后，汽车从A地到B地大约可以少走多少千米(结果精确到1千米)？(参考数据：≈1.4，≈1.7)

Answer 1

【答案】汽车从A地到B地比原来少走为27千米．

【解析】

过点C作AB的垂线CD，垂足为D，在直角△ACD中，解直角三角形求出CD的长度和AC的长度，在直角△CBD中，解直角三角形求出BD的长度，再求出AD的长度，进而求出汽车从A地到B地比原来少走多少路程．

过点C作AB的垂线CD，垂足为D，

∵AB⊥CD，sin30°＝，BC＝80千米，

∴CD＝BCsin30°＝80×＝40(千米)，

AC=≈56.4（千米），

∵cos30°=，BC=80（千米），

∴BD=BCcos30°=80×=40（千米），

∵tan45°=，CD=40（千米），

∴AD=40（千米），

∴AB=AD+BD=40+40≈40+40×1.73=109.2（千米），

∴汽车从A地到B地比原来少走多少路程为：AC+BC-AB=136.4-109.2=27.2≈27（千米）．

答：汽车从A地到B地比原来少走的路程为27千米．