题目内容
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
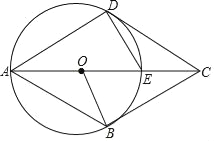
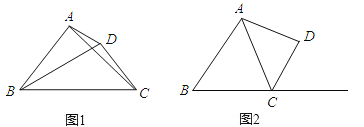
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
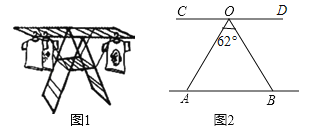
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
【答案】(1)④;(2)见解析;(3)存在这样一点E,使得四边形ABED为邻对等四边形,DE=![]()
【解析】
(1)根据中点四边形的特征,结合邻对等四边形的定义求解即可;
(2)延长CD至E,使CE=BA,根据“SAS”可证△ABC≌△ECB,从而BE=CA,∠BAC=∠E.利用等量代换可证BD=BE,从而∠BDE=∠E,然后可证明结论成立;
(3)在BC延长线上取一点E,使得CE=4,连接DE,四边形ABED即为邻对等四边形.连接AE,BD,由等腰三角形的性质和三角形外角的性质可证∠ABC=∠DEB,∠ACE=∠BCD.通过证明CE≌△BCD,可证BD=AE,从而四边形ABED为邻对等四边形.通过证明△ABC∽△DEC,利用相似三角形的性质可求出DE的长.
(1)①顺次连接任意四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
②顺次连接平行四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
③顺次连接矩形各边中点所得的四边形是菱形,菱形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
④顺次连接菱形各边中点所得的四边形是矩形,矩形具备一组邻角相等且对角线相等,故是邻对等四边形;
故答案为④;
(2)∵AB>CD,故可延长CD至E,使CE=BA,
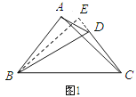
在△ABC与△ECB中,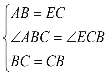 ,
,
∴△ABC≌△ECB.
∴BE=CA,∠BAC=∠E.
∵AC=DB,
∴BD=BE.
∴∠BDE=∠E.
∴∠CDB+∠BDE=∠CDB+∠E=∠BAC+∠CDB=180°.
即∠BAC与∠CDB互补.
(3)存在这样一点E,使得四边形ABED为邻对等四边形,
如图2,在BC延长线上取一点E,使得CE=4,
连接DE,四边形ABED即为邻对等四边形.
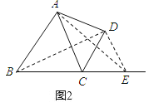
理由如下:
连接AE,BD,
∵CE=CD,
∴∠CDE=∠CED.
∵∠BCD=2∠B,
∴∠ABC=∠DEB,∠ACE=∠BCD.
在△ACE与△BCD中,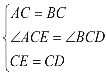 ,
,
∴△ACE≌△BCD.
∴BD=AE,四边形ABED为邻对等四边形.
∵∠CBA=∠CAB=∠CDE=∠CED,
∴△ABC∽△DEC.
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案