题目内容
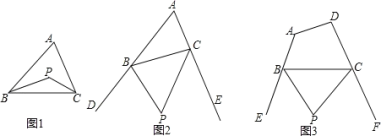
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
【答案】(1)125°;(2)∠BPC=90°﹣![]() ∠A,理由见解析;(3)∠BPC =180°﹣
∠A,理由见解析;(3)∠BPC =180°﹣![]()
【解析】
(1)借助角平分线的性质即可得到∠PBC=![]() ∠ABC以及∠PCB=
∠ABC以及∠PCB=![]() ∠ACB,然后在△BPC中进一步分析可找出∠BPC与∠A的关系,进而求出∠BPC的度数;
∠ACB,然后在△BPC中进一步分析可找出∠BPC与∠A的关系,进而求出∠BPC的度数;
(2)根据三角形内角和定理可知∠BPC=180°﹣(∠PBC+∠PCB),根据角平分线的定义可用![]() (∠DBC+∠ECB)表示∠PBC+∠PCB,再利用三角形外角性质得到∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,即可求出∠BPC与∠A的关系;
(∠DBC+∠ECB)表示∠PBC+∠PCB,再利用三角形外角性质得到∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,即可求出∠BPC与∠A的关系;
(3)延长BA、CD相交于点Q,由(2)的分析可直接得出∠P与∠Q的关系,而∠BAD与∠CDA是△ADQ的外角,再结合三角形外角性质即可解答.
(1)解:∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠A)
(180°﹣∠A)
=90°+![]() ∠A
∠A
=90°+35°
=125°
故答案为:125°
(2)∠BPC=90°﹣![]() ∠A
∠A
理由如下:
∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=180°﹣![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°﹣![]() (∠A+180°)
(∠A+180°)
=90°﹣![]() ∠A
∠A
(3)延长BA、CD相交于点Q,如图
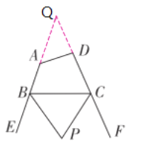
∠BPC=90°﹣![]() ∠Q
∠Q
∴∠Q=180°﹣2∠BPC
∴∠BAD+∠CDA=180°+∠Q=180°+180°﹣2∠BPC =360°﹣2∠BPC
∴∠BPC =180°﹣![]()
故答案为:∠BPC =180°﹣![]()

 备战中考寒假系列答案
备战中考寒假系列答案