题目内容
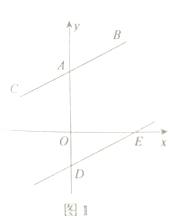
【题目】已知,点![]() ,点
,点![]() 分别在
分别在![]() 轴正半轴和负半轴上,
轴正半轴和负半轴上,![]() .
.
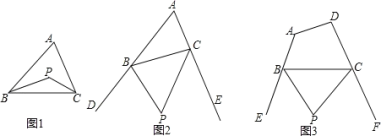
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在![]() 和
和![]() 内作射线
内作射线![]() ,
,![]() ,分别与过
,分别与过![]() 点的直线交于第一象限内的点
点的直线交于第一象限内的点![]() 和第三象限内的点
和第三象限内的点![]() .
.
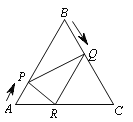
①如图2,若![]() ,
,![]() 恰好分别平分
恰好分别平分![]() 和
和![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,当
,当![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.

【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用二次根式的性质求得![]() 的值,根据三角形内角和定理结合已知条件构建方程,再利用平行线的性质即可求解;
的值,根据三角形内角和定理结合已知条件构建方程,再利用平行线的性质即可求解;
(2)①过M作MF∥AB,NG∥AB,根据角平分线的性质和平行线的性质,求得∠AMN-∠ENM =![]() –
–![]() ,再根据平行线的性质和三角形内角和定理即可求解;
,再根据平行线的性质和三角形内角和定理即可求解;
②设![]() ,
,![]() ,则
,则![]() ,
,![]() ,根据①的解法即可求得∠AMN-∠ENM=
,根据①的解法即可求得∠AMN-∠ENM=![]() ,再解不等式组即可求解.
,再解不等式组即可求解.
(1)∵![]() ,整理得:
,整理得:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴∠BAD=4∠OED,
∵∠OED+∠ODE=90![]() ①,∠BAD+∠ODE=180
①,∠BAD+∠ODE=180![]() ,即4∠OED +∠ODE=180
,即4∠OED +∠ODE=180![]() ②,
②,
联立①②解得:∠OED=30![]() ,∠ODE=60
,∠ODE=60![]() ,
,
∵AB∥DE,
∴∠CAD=∠ODE=60![]() ;
;
(2)①∵AM、EN是∠BAO、∠DEO的平分线,
∴设![]() ,
,![]() ,
,
过M作MF∥AB,NG∥AB分别交AD于F,G,
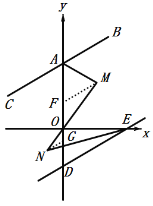
∵AB∥DE,
∴AB∥MF∥NG∥DE,
∴∠FMA=∠BAM=![]() ,∠FMN=∠MNG,∠GNE=∠NED=
,∠FMN=∠MNG,∠GNE=∠NED=![]() ,
,
∴∠AMN=∠FMA+∠FMN=![]() +∠FMN,
+∠FMN,
∠ENM=∠GNE +∠MNG =![]() +∠FMN,
+∠FMN,
∴∠AMN-∠ENM=![]() +∠FMN-
+∠FMN-![]() -∠FMN=
-∠FMN=![]() –
–![]() ;
;
∵∠ODE+∠OED=∠ODE+2![]() =90
=90![]() ,
,
∵AB∥DE,
∴∠BAD+∠ODE=180![]() ,即
,即![]() +∠ODE=180
+∠ODE=180![]() ,
,
∴![]() –
–![]() =90
=90![]() ,
,
∴∠AMN-∠ENM=![]() –
–![]() =45
=45![]() ;
;
②∵![]() ,
,![]() ,
,
∴设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
过M作MF∥AB,NG∥AB分别交AD于F,G,
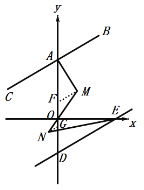
∵AB∥DE,
∴AB∥MF∥NG∥DE,
∴∠FMA=∠BAM=![]() ,∠FMN=∠MNG,∠GNE=∠NED=
,∠FMN=∠MNG,∠GNE=∠NED=![]() ,
,
∴∠AMN=∠FMA+∠FMN=![]() +∠FMN,
+∠FMN,
∠ENM=∠GNE +∠MNG =![]() +∠FMN,
+∠FMN,
∴∠AMN-∠ENM=![]() +∠FMN-
+∠FMN-![]() -∠FMN=
-∠FMN=![]() –
–![]() =
=![]() ;
;
∵∠ODE+∠OED=∠ODE+![]() =90
=90![]() ,
,
∵AB∥DE,
∴∠BAD+∠ODE=180![]() ,即
,即![]() +∠ODE=180
+∠ODE=180![]() ,
,
∴![]() –
–![]() =90
=90![]() ,即
,即![]() –
–![]() =
=![]() ,
,
∴∠AMN-∠ENM=![]() =
=![]() ;
;
∵![]() ,
,
∴![]() ,
,
解不等式![]() ,化简得:
,化简得:![]() ,
,
解得:![]() ,
,
解不等式![]() ,化简得:
,化简得:![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.

【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.