题目内容
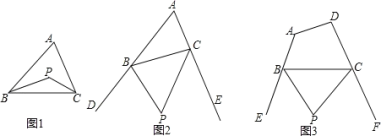
【题目】探究与发现:在△ABC中,∠B=∠C,点D在BC边上(点B、C除外),点E在AC边上,且∠ADE=∠AED,连接DE.
(1)如图①,若∠B=∠C=45,
①当∠BAD=60时,求∠CDE的度数;
②试猜想∠BAD与∠CDE的数量关系,并说明理由.
(2)深入探究:如图②,若∠B=∠C,但∠C≠45,其他条件不变,试探究∠BAD与∠CDE的数量关系.

【答案】(1)①∠CDE=30°;②∠BAD=2∠CDE,理由见解析;(2)∠BAD=2∠CDE.
【解析】
(1)①先根据三角形外角的性质得出∠ADC=∠B+∠BAD=105°,∠AED=∠EDC=75°,再由∠CDE=∠ADC-∠ADE即可得出结论;
②引入参数,设∠BAD=x,根据①的过程方法解答即可
(2)同(1)理,用角直接计算进行转化即可.
解:(1)①∵∠ADC是△ABD的外角,∠B=45°,∠BAD=60°,
∴∠ADC=∠BAD+∠B=60°+45°=105°,
∵∠B=∠C=45,
∴∠BAC=90°,
∠DAE=∠BAC﹣∠BAD=90°-60°=30°,
∴∠ADE=∠AED=![]() =
=![]() = 75°,
= 75°,
∴∠CDE=∠ADC-∠ADE =105°﹣75°=30°;
②∠BAD=2∠CDE,
理由如下:设∠BAD=x,
∴∠ADC=∠BAD+∠B=45°+x,
∵∠B=∠C=45,
∴∠BAC=90°,
∴∠DAE=∠BAC﹣∠BAD=90°﹣x,
∴∠ADE=∠AED=![]() =
=![]() ,
,
∴∠CDE=∠ADC-∠ADE =45°+x﹣![]() =
=![]() x,
x,
∴∠BAD=2∠CDE;
(2)设∠BAD=x,
∴∠ADC=∠BAD+∠B=∠B+x,
∵∠B=∠C,
∴∠BAC=180°﹣2∠C,
∴∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,
∴∠ADE=∠AED=![]() =
=![]() =∠C+
=∠C+![]() x,
x,
∴∠CDE=∠ADC-∠ADE=(∠B+x)﹣(∠C+![]() x)=
x)=![]() x,
x,
∴∠BAD=2∠CDE.

【题目】经测算,某地气温![]() 与距离地面的高度
与距离地面的高度![]() 有如下对应关系:
有如下对应关系:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表,完成下面的问题.
(1)猜想:距离地面的高度每上升![]() ,气温就下降______
,气温就下降______![]() ;表中
;表中![]() ______.
______.
(2)气温![]() 与高度
与高度![]() 之间的函数关系式是______.
之间的函数关系式是______.
(3)求该地距离地面![]() 处的气温.
处的气温.