题目内容
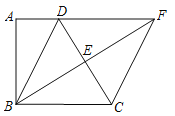
【题目】如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，点E为CD的中点，射线BE交AD的延长线于点F，连接CF．
（1）求证：四边形BCFD是菱形；
（2）若AD=1，BC=2，求BF的长．
【答案】（1）证明见解析（2）2
【解析】
（1）∵AF∥BC，∴∠DCB=∠CDF，∠FBC=∠BFD，
∵点E为CD的中点，∴DE=EC，
在△BCE与△FDE中，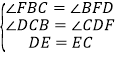
，
∴△BCE≌△FDE，∴DF=BC，
又∵DF∥BC，∴四边形BCDF为平行四边形，
∵BD=BC，∴四边形BCFD是菱形；
（2）∵四边形BCFD是菱形，∴BD=DF=BC=2，
在Rt△BAD中，AB=
，
∵AF=AD+DF=1+2=3，在Rt△BAF中，BF=
=2．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
